Multiple Constant Multiplication Algorithm
Multiple Constant Multiplication (MCM) is an arithmetic operation that multiplies a set of fixed-point constants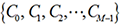 
with the same fixed-point variable X. From a circuit point of view, MCM dominates the complexity of the whole category of Linear Time Invariant (LTI) systems, such as, FIR/IIR filters, DSP transforms (DCT, DFT, Walsh, …), LTI controllers, crypto-systems, etc. To be efficiently implemented, MCM must avoid costly multipliers. The hardware alternative must be multiplierless, i.e., using only additions, subtractions, and shifts. Therefore, the MCM problem is defined as the process of finding the minimum number of addition/subtraction operations. The computational complexity of MCM is conjectured to be NP-hard.
Because of the increasing demand in high-speed and low-power design, MCM problem has been the focus of important researches during these last three decades. As a result, a big number of MCM algorithms have been proposed, mostly based on the acyclic directed graphs, or common subexpression elimination, or the combination of both together.
We propose hereafter a new MCM algorithm, called RADIX-2r, for it is essentially based on the radix-2r arithmetic. It has the merit over the existing MCM algorithms of being:
Fully predictable
The upper-bound (Upb) in number of additions, adder-depth (Ath), and average (Avg), are known with exact analytic formulas. This feature not only allows designers to get a pre-implementation picture on area, speed and power, but it also enables synthesis tools to rapidly satisfy user constraints and perform necessary tradeoffs without the "endless" feedbacks looking for the appropriate solution. Note that none of the existing MCM algorithms is predictable in Upb, Ath, or Avg.
Sublinear
For a given number M of nonnegative constants with a bit-length N, RADIX-2r exhibits a sublinear runtime-complexity O(M×N/r), where r is a function of (M, N). This means that it has no limitation regarding the couple (M, N). For high-complexity problems (M×N>>), RADIX-2r is most likely the only one that is even feasible to run. Note that the best MCM heuristics have either a polynomial or exponential complexity.
High-speed and low-power solution
Adder-depth (Ath) is not only a measure of the critical-path (speed), but also a good indicator of the power consumption. It has been proved in many papers that a lower Ath results in lower power consumption due to the limitation of the glitch propagation. The existing MCM algorithms can not compete with RADIX-2r because it allows a logarithmic reduction of Ath, while it is not possible in the other algorithms due to the shared additions.
One direct application of RADIX-2r for instance, is in the wireless communication where the filters employed in the receiver circuit of mobile systems must be of higher order (up to 800 taps) and must be realized to consume less power and operate at high speed.
